
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。 在振幅的对数对角频率的波特图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
一阶巴特沃斯滤波器的衰减率为每倍频6分贝,每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。巴特沃斯滤波器的振幅对角频率单调下降,并且也是唯一的无论阶数,振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高,在阻频带振幅衰减速度越快。其他滤波器高阶的振幅对角频率图和低级数的振幅对角频率有不同的形状。
设计步骤如设计一个数字低通滤波器,其技术指标为:
通带临界频率fp ,通带内衰减小于rp;
阻带临界频率fs,阻带内衰减大于αs;采样频率为FS
1、将指标变为角频率 wp=fp*2*pi;ws= fs*2*pi;
2、将数字滤波器的频率指标{Wk}由wk=(2/T)tan(Wk/2)转换为模拟滤波器的频率指标{wk},由于是用双线性不变法设计,故先采取预畸变。

3、将高通指标转换为低通指标,进而设计高通的s域模型
4、归一化处理
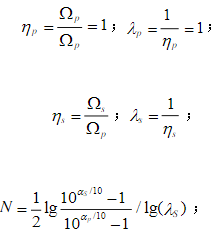
由以上三式计算出N,查表可得模拟低通滤波器的阶数,从而由下式确定模拟高通滤波器的参数。
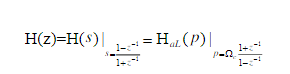
| 欢迎光临 EDA365电子论坛网 (https://bbs.eda365.com/) | Powered by Discuz! X3.2 |